Dieses Kapitel gibt eine kleine Einführung in
zweidimensionale Rastergrafik.
Dabei geht es darum, zweidimensionale Objekte wie Linien, Dreiecke
oder Polygone möglichst effizient auf einem
Ausgabegerät
darzustellen, das wie ein Computerbildschirm in rechteckige
Punkte aufgeteilt, also gerastert, ist. Die rechteckigen,
meist quadratischen Punkte heißen Pixel (Kurzform von picture
elements).
Aufgrund ihrer Geschwindigkeit wollen wir scan
conversion
Algorithmen verwenden. Dabei wird ein Objekt in horizontaler (oder
vertikaler) Richtung entlang des Punkterasters abgefahren (ge-"scant").
Die zu setzenden Punkte werden dann für alle Zeilen (oder
Spalten)
der Reihe nach ermittelt und gezeichnet.
Die beigefügten Beispiele in PASCAL sind getestet
worden. Es
kann dennoch vorkommen, daß sich hier oder dort ein
Tippfehler
eingeschlichen hat.
|
Nehmen wir an, wir möchten eine Linie vom
Startpunkt (x1,y1)
zum Endpunkt (x2,y2)
ziehen.
Vereinfachend
gehen wir davon aus, daß die Linie relativ "steil" ist, also |x2-x1|
< |y2-y1|
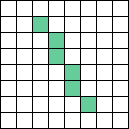
gilt. Aufgrund
der Steilheit müssen wir eine y-Schleife benutzen
und für jedes y in der entsprechenden x-Spalte des Bildes einen Punkt
setzen (siehe Abbildung).Vereinfachen
unsere
Betrachtungen weiter, indem wir annehmen, dass wir von oben nach unten
zeichnen, also y1 < y2
ist. Der einfachste Linien-Algorithmus in Pascal sieht dann wie folgt
aus:
|
|
procedure Line1(x1, y1, x2, y2, color: integer);
var
y : integer;
x,m : real;
begin
m := (x2-x1) / (y2-y1);
for y := 0 to (y2-y1) do
begin
x := m*y + x1;
WritePixel (round(x), y+y1, color)
end
end; { Line1 }
Oder in C++:
void Line1(int x1, int y1, int x2, int y2, int color)
{
int y;
float x, m;
m = float(x2-x1) / float(y2-y1);
for (y = 0; y < y2-y1; y++)
{
x = m*y + x1;
WritePixel (int(x+0.5f), y+y1, color);
}
} // Line1
Das ist leider absolut ineffizient, da wir für
jeden zu
setzenden Punkt eine Multiplikation, zwei Additionen und eine Rundung
benötigen.
Die Multiplikation und eine Addition können wir
sparen, indem
wir x vor der der Schleife mit x1
initialisieren und bei jedem y-Durchlauf nur noch m
auf x
addieren. In Pascal:
procedure Line2(x1, y1, x2, y2, color: integer);
var
y : integer;
x,m : real;
begin
m := (x2-x1) / (y2-y1);
x := x1;
for y := y1 to y2 do
begin
WritePixel (round(x), y, color);
x := x + m
end
end; { Line2 }
Und in C++:
void Line2(int x1, int y1, int x2, int y2, int color)
{
int y;
float x, m;
m = float(x2-x1) / float(y2-y1);
x = x1;
for (y = y1; y <= y2; y++)
{
WritePixel (int(x+0.5f), y, color);
x = x + m;
}
} // Line2
Trotzdem müssen wir hier für jeden Punkt
einmal runden.
Außerdem ist das Rechnen mit Gleitkommazahlen meist langsamer
als
das mit Festkommazahlen.
Um nur noch mit Festpunktzahlen rechnen zu
müßen, sind
zwei logische Schritte nötig. Erst einmal teilen wir die
Gleitkommazahlen x und m
in Vorkomma- und
Nachkomma-Teil auf. Bei jedem Schleifendurchlauf addieren wir nun diese
beiden Teile separat. Ergibt sich beim Nachkommateil ein
Überlauf,
so addieren wir ihn noch auf den Vorkomma-Teil.
Um das Runden leichter zu machen, starten wir mit einem
Nachkomma-Teil von -0,5 und vereinfachen damit zusätzlich noch
die
Übertrags-Bedingung. In Pascal:
procedure Line3(x1, y1, x2, y2, color: Integer);
var
y : integer;
xi, mi : integer; { i für integer (Vorkomma-Teil) }
xf, mf : real; { f für float (Nachkomma-Teil) }
begin
xi := x1;
xf := -0.5;
mi := (x2-x1) div (y2-y1);
mf := (x2-x1) / (y2-y1) - mi;
for y := y1 to y2 do
begin
WritePixel (xi, y, color);
xi := xi + mi;
xf := xf + mf;
if xf > 0.0 then { ergibt sich ein Übertrag? }
begin
xi := xi + 1;
xf := xf - 1.0
end
end
end; { Line3 }
In C++:
void Line3(int x1, int y1, int x2, int y2, int color)
{
int y;
int xi, mi; // i für integer (Vorkomma-Teil)
float xf, mf; // f für float (Nachkomma-Teil)
xi = x1;
xf = -0.5;
mi = (x2-x1) / (y2-y1);
mf = float(x2-x1) / float(y2-y1) - float(mi);
for (y = y1; y <= y2; y++)
{
WritePixel(xi, y, color);
xi = xi + mi;
xf = xf + mf;
if (xf > 0.0) // ergibt sich ein Übertrag?
{
xi = xi + 1;
xf = xf - 1.0;
}
}
} // Line3
Jetzt ist der Nachkomma-Teil unabhängig vom
Vorkomma-Teil, so
daß wir ihn mit 2*(y2-y1)
durchmultiplizieren können, und nur noch mit Festkommazahlen
arbeiten müssen.
Procedure Line4(x1, y1, x2, y2, color: integer);
var
y : integer;
xi,mi : integer;
xf,mf : integer;
begin
xi := x1;
xf := -(y2-y1);
mi := (x2-x1) div (y2-y1);
mf := ((x2-x1) mod (y2-y1))*2;
for y := y1 to y2 do
begin
WritePixel (xi, y, color);
xi := xi + mi;
xf := xf + mf;
if xf > 0 then { ergibt sich ein Übertrag? }
begin
xi := xi + 1;
xf := xf - 2*(y2-y1)
end
end
end; { Line4 }
In C++:
void Line4(int x1, int y1, int x2, int y2, int color)
{
int y;
int xi, mi;
int xf, mf;
xi = x1;
xf = -(y2-y1);
mi = (x2-x1) / (y2-y1);
mf = ((x2-x1) % (y2-y1))*2;
for (y = y1; y <= y2; y++)
{
WritePixel (xi, y, color);
xi = xi + mi;
xf = xf + mf;
if (xf > 0) // ergibt sich ein Übertrag?
{
xi += 1;
xf -= 2*(y2-y1);
}
}
} // Line4
Der Term 2*(y2-y1) kann vor dem
Aufruf der Schleife
berechnet werden, da er konstant bleibt.
Natürlich kann auch x die Laufvariable sein. Wir
haben hier
ja nur den Spezialfall mit |x2-x1|
< |y2-y1|
und y2-y1 > 0
betrachtet. Um einen
kompletten Linienalgorithmus zu schreiben, benötigt man also
noch
eine Fallunterscheidung, die je nach Eingabe in unterschiedliche
Unterteile verzweigt.
Der Bresdenham-Algorithmus hat die unschöne
Eigenschaft,
dass ein Verzweigungspunkt darin vorkommt.
Festkommazahlen lassen sich auch in einer einzigen
Integer-Zahl
codieren, die dann sowohl den Vorkomma- als auch den Nachkommateil
enthält. Die höherwertigen Bits dienen dabei als
Festkommateil, die niederwertigen Bits als Nachkommateil. Wie bei
anderen Festkommazahlen ist hier besondere Achtung vor Über- oder
Unterläufen aufgrund der beschränkten Genauigkeit
(Anzahl der
Bits) geboten.
Sagen wir, die unteren zehn Bit einer Zahl dienen als
Nachkommastellen,
d.h. Bit 10 repräsentiert 0.5, Bit 9 repräsentiert
0.25 usw.
Dann
lässt sich der Linienalgorithmus Line2 in C++ auch so
formulieren
(und
zwar wirklich optimiert):
void Line5(const int x1, const int y1, const int x2, const int y2, const int color)
{
static regsiter const int SHIFT = 10;
static regsiter const int ROUND = (1<<(SHIFT-1));
register int y;
register const int m = (((x2-x1) << SHIFT) + ROUND) / (y2-y1);
regsiter int x = (x1 << SHIFT) + ROUND;
for (y = y1; y <= y2; ++y)
{
WritePixel ((x >> SHIFT), y, color);
x = x + m;
}
} // Line5
Das sieht auf den ersten Blick komplizierter aus, als es
ist,
funktioniert aber wunderbar. Wir haben m
durch
eine schön gerundete Division errechnet. Auch die korrekte
Rundung
von x
für WritePixel()
haben wir durch Addition von ROUND bei der Initialisierung von x
mit x1
schon
oben sichergestellt. Also: Alles paletti für eine
Zeichenroutine
mit einem Shift und einer Addition.
Für |x2-x1|=|y2-y1|
= 0 ergibt sich ein Punkt. Um noch mehr Geschwindigkeit zu erreichen,
kann man weiterhin die Spezialfäle einer horizontalen und
vertikalen Linie isolieren. Mit dx = x2-x1
und dy
= y2-y1 gilt:
1. dx = 0, dy = 0 => Punkt
2. dx = 0 => vertikale Linie
3. dy = 0 => horizontale Linie
4. |dx| < |dy|, dy > 0 => Algorithmus mit y-Schleife
5. |dx| < |dy|, dy < 0 => Punkte vertauschen ... Algorithmus mit y-Schleife
6. |dx| > |dy|, dx > 0 => Algorithmus mit x-Schleife
7. |dx| > |dy|, dx < 0 => Punkte vertauschen ... Algorithmus mit x-Schleife
- Programmiere eine vollständige Linien-Routine,
die
alle Spezialfälle (vom Abschneiden am Bildschirmrand einmal
abgesehen) richtig auswertet und eine Linie entsprechend zeichnet.
Der Algorithmus geht davon aus, daß die Linie
genau in der
Mitte eines Pixels beginnt und in der Mitte eines anderen Pixels endet.
Das hat zur Folge, daß in der Anfangs- und Endreihe stets nur
ein
Pixel gezeichnet wird. Hat man eine genauere Position des Anfangs- und
Endpunkts zur Verfügung, so kann man diese Information
über
den Nachkommateil in den Algorithmus einbringen. Das Zeichnen einer
Linie z.B. von (19.4, 21.7) nach (40.3, 25.6) anstatt von (19, 22) nach
(40, 26) wird damit genauer.
Möchte
man mehrere Linien in einem Zug zeichnen, empfiehlt es sich, den
letzten Punkt einer Linie wegzulassen, damit er nicht doppelt gesetzt
wird. Würden beim Setzen des Punktes z.B. Farbwerte aufaddiert,
erhielte man einen doppelt so hellen Punkt an jeder Ecke des
Linienzuges.
Für alle Arten von Kommentaren bin ich
äußerst
dankbar. Fragen beantworte ich gerne.
[FOLEY92]
|
James D. Foley, Andries van Dam, Steven K. Feiner,
John F.
Hughes
"Computer Graphics: Priniples and Practice" - 2nd ed.
Addison-Wesley Publishing Company, Reading, Massachusetts, 1992
ISBN 0-201-12110-7
|
[WATT89]
|
Alan H. Watt
"Fundamentals of Three-Dimensional Computer-Graphics"
Addison-Wesley Publishing Company, Reading, Massachusetts, 1989
ISBN 0-201-15442-0
(there is a newer edition) |
Linien | Dreiecke
| Volumendarstellung
| Iteratives 3D
Füllen
home
