Abb. 1
| Gebiet | Volume Rendering | |
| Thema | Dreidimensionaler flood fill | |
| Autor | Holger Förterer | |
| Datum | 12. Mai 1995 | |
| Letzte Änderung | 3. Juni 2003 | |
| Version | 0.32b | |
2.2.1 Einleitung
2.2.2 Grenzen
2.2.3 Der zweidimensionale Fall
2.2.4 Beschleunigung der Methode im zweidimensionalen Fall
2.2.5 Erweiterung auf die dritte Dimension
2.2.6 Abschließende Bemerkungen
Dreidimensionales Füllen kann bei Computertomographiebildern eingesetzt werden, um Organe in einem medizinischen Bild zu isolieren. Ausgehend von einem Startpunkt, dem sogenannten "seedpoint" füllt man einen Teil des dreidimensionalen Grauwertvolumens aus. Hierzu eignen sich bei größeren Bildern rekursive Methoden nur bedingt, daher möchte ich hier einen einfachen iterativen Algorithmus vorstellen. Er wurde zwar von mir entwickelt, es gab jedoch mit an Sicherheit grenzender Wahrscheinlichkeit schon vorher ähnliche Algorithmen.
Wichtig ist natürlich zuerst die Frage, wie der zu füllenden Bereich begrenzt wird. Prinzipiell läßt sich dazu jedes beliebige Kriterium verwenden. In der Praxis hat es sich als brauchbar erwiesen, einen dreidimensionalen Gradienten zu verwenden. Steigt der Wert des Gradienten an einer Stelle über einen bestimmten Schwellwert, so handelt es sich um einen Grenzvoxel.
Einfacher ist es, alle Voxel in einem bestimmten Grauwertbereich um den Wert des seedpoints herum zu füllen. Der Bereich kann durch einen einfachen Schwellwert bestimmt werden. Alle Voxel im Intervall
[Grauwert - Schwellwert, Grauwert + Schwellwert]
gehören dann zum möglichen Füllvolumen, alle anderen betrachten wir als Grenzvoxel. Mit dem Schwellwert 0 kann man also auch gezielt bestimmte Grauwerte einzeln ausfüllen.
Beginnen wir mit etwas Einfachem, dem Algorithmus für zwei Dimensionen. Ich werde zunächst die einfache Idee hinter dem Algorithmus beschreiben, bevor ich zu Beschleuningungsmaßnahmen komme.
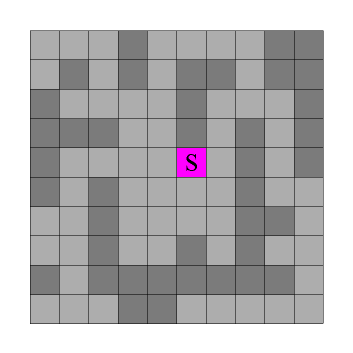
Wir gehen von einer Grauwertfläche aus, in der wir interaktiv einen Startpunkt S gewählt haben (Abb. 1). Die dunklen Pixel stehen hier für Grenzpixel, die hellen Pixel sollen gefüllt werden.
Ausgangssituation

Abb. 1
Ich möchte das Verfahren nun anhand eines Testlauf mit diesem Beispiel beschreiben (Abbildungen 2 und 3). Im ersten Schritt "verschmiere" ich den seedpoint S in x-Richtung, bis ich an Grenzpixel stoße. Ich fülle also nach links und nach rechts jeweils soweit, bis ein Grenzpixel erreicht wird. Die hierbei neu entstandenen Pixel sind in Abb. 2, Bild 1 gelb markiert.
Im nächsten Schritt "verschmiere" ich die so entstandene Pixelreihe in y-Richtung. Die hierbei neu entstandenen Pixel sind im zweiten Bild gelb eingefärbt. Nun "verschmiere" ich abwechselnd weiter in x- und y-Richtung, bis keine neuen Pixel mehr gefüllt werden (Bilder 3 bis 8).
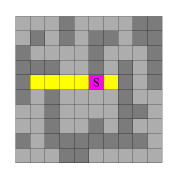
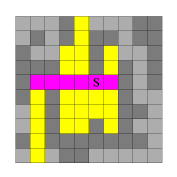
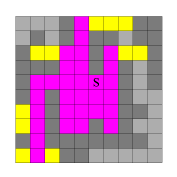
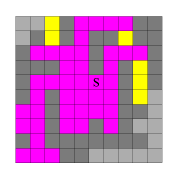
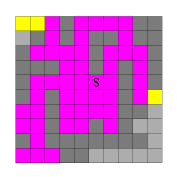
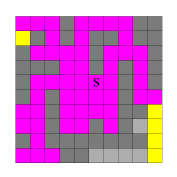
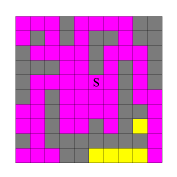
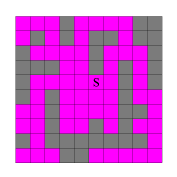
Abb. 2

Abb. 3
Wie man leicht sehen kann, ist der Algorithmus für feine Strukturen nicht gut geeignet. Allerdings sollte sich die Segmentierung von solch feinen Strukturen mit einem dreidimensionalen Füllalgorithmus ohnehin sehr schwierig gestalten, da sie oft durch eine zu geringe Auflösung der Scans selbst in sehr viele kleine Teile aufgespalten sind.
Das Füllverfahren sieht als intuitiver Pseudocode so aus (die x-Achse gehe von links nach rechts, die y-Achse von unten nach oben):
Fülle seedpoint
Wiederhole bis kein neuer Punkt gefüllt wurde
{
// Iteration in x-Richtung
Für alle y von unten bis oben wiederhole
Für alle x von links nach rechts wiederhole
Wenn (Pixel[x,y] gefüllt) dann
{
suche linken und rechten Endpunkt
Fülle vom linkem Endpunkt bis Pixel[x-1,y]
Fülle von Pixel[x+1,y] bis zum rechten Endpunkt
Bewege x hinter das rechte Ende
}
Wenn kein Punkt gefüllt wurde, verlasse Hauptschleife
// Iteration in y-Richtung
Für alle x von links nach rechts wiederhole
Für alle y von unten nach oben wiederhole
Wenn (Pixel[x,y] gefüllt) dann
{
suche unteren und oberen Endpunkt
Fülle vom unterem Endpunkt bis Pixel[x,y-1]
Fülle von Pixel[x,y+1] bis zum oberen Endpunkt
Bewege y unter das untere Ende
}
} // Ende der Hauptschleife
Insgesamt wurde das Volumen jetzt achtmal komplett (einige Voxel dabei doppelt) durchsucht, was alles andere als effektiv ist. Also kommen wir nun zu den Beschleunigungsverfahren.
Zur einfacheren Veranschaulichung habe ich beim Ansprechen von
Arrays die Reihenfolge x,y,z gewählt. Voxel[x,y,z]
bezeichnet also den Grauwert an der Stelle x,y,z im
Grauwertvolumen. Aufgrund der Art und Weise, wie die meisten
Programmiersprachen Arrays ablegen, sollte man allerdings bei der
Implementierung die Indizes umdrehen, also z.B. Voxel[z,y,x]
verwenden.
Zuerst einmal ist es nicht nötig, für jeden gefüllten Punkt rückwärts nach der linken bzw. unteren Grenze zu suchen. Da wir bei der Suche sowieso im Moment jeden Pixel durchlaufen, können wir uns merken, ob und wo die letzte Grenze zum füllbarem Bereich überschritten wurde.
Dazu brauchen wir eine Flagge (flag), die angibt,
ob ein solcher Grenzübergang stattgefunden hat, sowie die
Position (x1) dieses Übergangs. Als Pseudocode für
die Iteration in x-Richtung erhalten wir somit:
neu = 0; // Anzahl neuer Pixel
Für alle y von 0 bis maxY wiederhole
{
flag = false; // Grenzübergang stattgefunden?
x1 = 0; // Position des Grenzübergangs
x = 0;
Wiederhole solange (x <= maxX)
{
Falls Pixel[x,y]
gefüllt : {
Wenn (flag == true) {
Fülle von Pixel[x1,y] bis Pixel[x-1,y];
neu = neu + (x - 1) - x1 + 1;
flag = false;
}
Wiederhole solange (x+1 <= maxX) und
(Pixel[x+1,y] zu füllen) {
fülle Pixel[x+1,y];
neu = neu + 1;
x = x + 1;
}
}
zu füllen : Wenn (flag == false) {
x1 = x;
flag = true;
}
Grenzpixel : flag = false;
x = x + 1;
}
}
Wenn (neu = 0) dann verlasse Hauptschleife;
Die Routine für die Iteration in y-Richtung funktioniert ganz analog.
Betrachten wir nochmal das Bild, das sich nach der ersten Iteration ergeben hat (Abb. 3). Nur in den Spalten, in denen neu gefüllte Pixel hinzugekommen sind, ist es notwendig, in y-Richtung zu füllen. In der Abbildung sind die betreffenden Spalten durch Pfeile markiert. Als Besonderheit kommt bei der ersten y-Iteration die Spalte des Seedpoints hinzu.
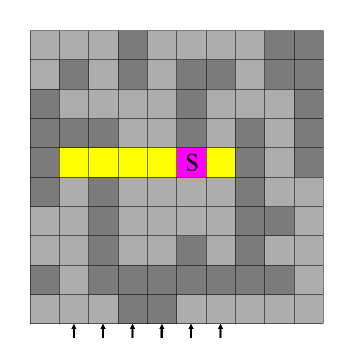
Abb. 3
Um uns die betreffenden Spalten bzw. Zeilen zu
merken, legen wir zwei boole'sche Arrays (BeschX und
BeschY) an. An den Stellen, an denen neu gefüllte
Pixel entstanden sind, schreiben wir true in den
Array für die nächste Iteration. Bei der Iteration in
x-Richtung aktualisieren wir also BeschY und
andersherum. Dadurch sparen wir uns auf einfache Weise unnötige
Arbeit:
neu = 0; // Anzahl neuer Pixel
Für alle y von 0 bis maxY wiederhole
Wenn (BeschX[y] == true) dann // Zeile untersuchen?
{
BeschX[y] = false; // setze zurück
flag = false; // Grenzübergang stattgefunden?
x1 = 0; // Position des Grenzübergangs
x = 0;
Wiederhole solange (x <= maxX)
{
Falls Pixel[x,y]
gefüllt : {
Wenn (flag == true) {
// Fülle von Pixel[x1,y] bis Pixel[x-1,y]
xx = x1;
Wiederhole solange (xx < x) {
Fülle Pixel[xx,y];
BeschY[xx] = true;
neu = neu + 1;
xx = xx + 1;
}
flag = false;
}
Wiederhole solange (x+1 <= maxX) und
(Pixel[x+1,y] zu füllen) {
fülle Pixel[x+1,y];
BeschY[x+1] = true;
neu = neu + 1;
x = x + 1;
}
}
zu füllen : Wenn (flag == false) {
x1 = x;
flag = true;
}
Grenzpixel : flag = false;
x = x + 1;
}
}
Wenn (neu = 0) dann verlasse Hauptschleife;
Für den dreidimensionalen Fall füllen wir in x-, y- und z-Richtung. Der Algorithmus für das Füllen selbst ändert sich dabei nicht grundlegend, allerdings dürfen wir die Berechnung jetzt erst abbrechen, wenn die letzten beiden Iterationen keine neu gefüllten Voxel mehr ergeben haben.
Desweiteren müssen die oben angesprochenen Arrays Besch?
zur Bestimmung der zu untersuchenden Spalten, Zeilen oder
"Tiefen" nun zweidimensional programmiert werden. Zur
Verdeutlichung gebe ich nochmals den Pseudocode zur Iteration in
x-Richtung an:
Vorbelegte Variablen:
alt : Anzahl der Pixel, die in der letzten Iteration gefüllt wurden.
gesamt : Anzahl insgesamt gefüllter Pixel (z.B. zur Volumenberechnung)
iterat : Anzahl der komplett ausgeführten Iterationen
neu = 0; // Anzahl neu gefüllter Pixel
Für alle z von 0 bis maxZ wiederhole
Für alle y von 0 bis maxY wiederhole
Wenn (BeschX[y,z] == true) dann // Zeile untersuchen?
{
BeschX[y,z] = false; // setze zurück
flag = false; // Grenzübergang stattgefunden?
x1 = 0; // Position des Grenzübergangs
x = 0;
Wiederhole solange (x <= maxX)
{
Falls Voxel[x,y,z]
gefüllt : {
Wenn (flag == true) {
// Fülle Voxel[x1,y,z] bis Voxel[x-1,y,z]
xx = x1;
Wiederhole solange (xx < x) {
fülle Voxel[xx,y,z];
BeschY[xx,z] = true;
BeschZ[xx,y] = true;
neu = neu + 1;
xx = xx + 1;
}
flag = false;
}
Wiederhole solange (x+1 <= maxX) und
(Pixel[x+1,y,z] zu füllen)
{
fülle Voxel[x+1,y,z];
BeschY[x+1,z] = true;
BeschZ[x+1,y] = true;
neu = neu + 1;
x = x + 1;
}
}
zu füllen : Wenn (flag == false) {
x1 = x;
flag = true;
}
Grenzpixel : flag = false;
x = x + 1;
}
}
Wenn (iterat > 2) und (alt+neu == 0) dann verlasse Hauptschleife
gesamt = gesamt + neu;
alt = neu;
iterat = iterat + 1;
Im Hauptprogramm ergibt sich folgendes Aufrufschema:
fülle BeschX, BeschY und BeschZ mit false // Initialisierung
fülle Voxel[seedx,seedy,seedz] // fülle seedpoint
BeschX[seedy,seedz] = true;
BeschY[seedx,seedz] = true;
BeschZ[seedx,seedy] = true;
gesamt = 1;
alt = 1;
iter = 0;
Wiederhole // Hauptschleife
{
Iteration in x-Richtung;
Iteration in y-Richtung;
Iteration in z-Richtung;
} // Ende der Hauptschleife
Die Ausführung kann noch weiter beschleunigt werden, indem man nicht nur ein
Flag wie in BeschX verwendet, sondern sich zusätzlich Minimum und
Maximum der neu erstellten Voxel in jeder Zeile merkt. So müssen große Teile
der Zeile nicht durchsucht werden. Man durchsucht sie nur vom Minimum bis zum
Maximum. Diese Methode macht allerdings ein Rückwärtssuchen notwendig und der
Code wird zu komplex, um noch anschaulich zu sein. Daher verzichte ich hier
darauf, explizit einen Pseudocode anzugeben. Ausserdem steigt der Speicherbedarf
deutlich an. Ziel war hier auch nur, einen schlanken, verständlichen Algorithmus
zu skizzieren.
Ich erhebe keinen Anspruch auf eine Fehlerfreiheit dieser Beschreibung. Genausowenig glaube ich, daß es nicht bessere bzw. schnellere Methoden gibt. Für Hinweise auf noch so kleine Fehler und für andere Anregungen bin ich aber immer dankbar.
Ich habe mich bemüht, den Algorithmus so einfach wie möglich zu beschreiben. Sollte mir das nicht gelungen sein, dann wäre ich über ein Feedback froh, damit ich den Text verbessern kann und er in Zukunft verständlicher wird.
Linien | Dreiecke | Volumendarstellung | Iteratives 3D Füllen