I)
t)
(Raytracing)
| Gebiet | Volume Rendering | |
| Thema | Darstellung transparenter Grauwertvolumen | |
| Autor | Holger Förterer | |
| Datum | 4. März 1994 | |
| Letzte Änderung | 27. Mai 2006 | |
| Version | 0.32d | |
Dieses Kapitel beschreibt einen einfachen Algorithmus zur Darstellung von Grauwertvolumen, wie sie zum Beispiel beim Computertomographie (CT) Verfahren entstehen. Der Algorithmus basiert auf der Methode der Strahlenverfolgung (Raytracing), deren Grundprinzipien in [WATT89] gut beschrieben sind. Da ich selbst Dinge besser verstehe, wenn sie in Diagrammen dargestellt werden, habe ich meine Ausführungen möglichst umfangreich illustriert.
Grundkenntnisse im Umgang mit Vektoren und das Lesen einfacher Computeranweisungen sind eine Grundvoraussetzung für dieses Kapitel. Viel mehr brauchen wir nicht.
Das Kapitel ist leider etwas länger geworden als ursprünglich von mir geplant. Es wäre viel kürzer, wenn ich mich nicht damit aufgehalten hätte, alle Probleme konkret zu lösen. Doch es war mir wichtiger, die zahlreichen Fakten zusammenzutragen, als es mir leicht zu machen und einfach zu erklären, "dass man das irgendwie machen solle". Ich befinde mich damit leider in gewisser Weise im Widerstreit mit meiner eigentlichen Idee, alles so schlank und einfach wie möglich zu gestalten.
Bevor ich mit der Beschreibung des Algorithmus beginne, möchte ich einige oft verwendete Begriffe erläutern:
| Voxel | In diesem Kontext ein Würfel mit einer einzigen Farbe, eine Art dreidimensionaler Pixel. Voxel ist eine Kurzform für volume element. Ich betrachte hier der Einfachheit halber nur Voxel der Kantanlänge 1, also Einheitswürfel. | |
Grauwert (I)
|
Ein Helligkeitswert (eine Licht Intensität) von 0.0 (schwarz) bis 1.0 (weiß). | |
Transparenz (t)
|
Ein Lichtdurchlässigkeitswert von 0.0 (undurchsichtig) bis 1.0 (durchsichtig, voll transparent). | |
| Grauwertvolumen | Ein dreidimensionaler Quader, der vollständig aus verschieden transparenten Voxeln grauer Farbe besteht. | |
| Augpunkt | Die mathematische Position des Auges, durch das der Betrachter das Grauwertvolumen sieht, oft auch Blickpunkt genannt. | |
| Strahlenverfolgung (Raytracing) |
Methode, bei der vom Augpunkt aus durch jeden Pixel des Bildschirms ein Strahl geschossen wird. Die Farbe eines Pixels hängt davon ab, auf was sein Strahl trifft. |
Der Einfachheit halber gehen wir im Folgenden davon aus, dass sich der Augpunkt außerhalb des Grauwertvolumens befindet. Nun schicken wir der Reihe nach durch jeden Pixel des zu berechnenden Bildes einen Strahl. Für jeden Strahl gibt es zwei Möglichkeiten: Entweder er trifft das Grauwertvolumen oder nicht. Dies festzustellen, ist der erste Schritt.
um aus diesen beiden Informationen die Farbe des Pixels zu errechnen.
Ich werde zusätzlich noch einige Worte über die Transparenz der Voxel verlieren.
Im ersten Schritt versuchen wir also zu ermitteln, ob und wo der Strahl das Grauwertvolumen trifft. Das Volumen wird durch sechs Rechtecke begrenzt (Abb. 1). Wir schneiden nun den Strahl der Reihe nach mit jedem dieser Rechtecke. Wie geschieht dies? Jedes Rechteck ist ein Teil einer Ebene. Wir schneiden zuerst den Strahl mit der Ebene, in der das Rechteck liegt. Danach überprüfen wir, ob dieser Schnittpunkt innerhalb der Grenzen des Rechtecks liegt. Schließlich müssen wir noch berechnen, ob der Strahl beim Schnittpunkt in das Grauwertvolumen eintaucht oder aus ihm austritt.
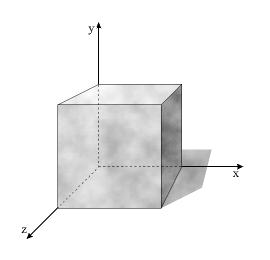
Abb. 1
Der Einfachheit halber gehe ich davon aus, dass die sechs Rechtecke, wie in der Abbildung, zur xy-, xz- bzw. yz-Ebene parallel verlaufen. Sehen wir uns beispielsweise an, wir der Schnitt mit dem roten Rechteck in Abbildung 2 berechnet werden kann.
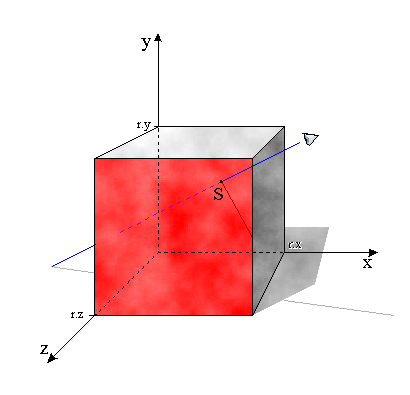
Abb. 2
Die Ebene, in der das rote Rechteck liegt, ist durch die
z-Koordinate ihrer Punkte bestimmt, x- und y-Koordinate sind
beliebig. Sei für das rote Rechteck z = r.z mit
einem bestimmten r.z. Weiterhin seien der Augpunkt A
:= (a.x, a.y, a.z) und die
Strahlrichtung ![]() := (
:= (d.x, d.y, d.z)
bekannt. Aufgrund des Strahlensatzes (Abb. 3) folgt nun für die
Koordinaten des Schnittpunkts S := (s.x, s.y,
s.z) mit (d.z ![]() 0):
0):
s.x = a.x + (d.x / d.z) * (r.z - a.z)
s.y = a.y + (d.y / d.z) * (r.z - a.z)
s.z = r.z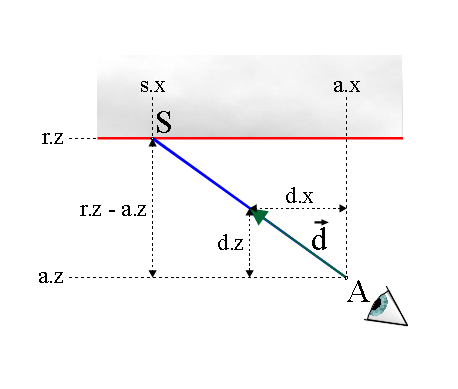
Abb. 3
Wenn d.z = 0 ist, so ist es aus praktischen
Gründen sinnvoll, festzulegen, dass sich Rechteck und Strahl
nicht schneiden. Der wahre Schnitt würde unter Umständen aus
einer ganzen Strecke bestehen. Doch was würde wir mit dieser
Information anfangen? In diesem Fall ist es sinnvoller, die zwei
Schnittpunkte mit den angrenzenden Seiten als Eintrittspunkt S
und Austrittspunkt E zu betrachten (Abb. 4).
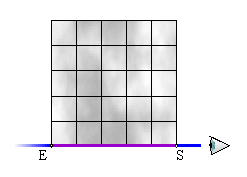
Abb. 4
Wir haben den Schnittpunkt mit der Ebene, in der das Rechteck liegt, ermittelt. Die Grenzen des roten Rechtecks sind in unserem Beispiel (Abb. 2) durch
0 <= x <= r.x und 0
<= y <= r.y
gegeben. Wir überprüfen nun die Koordinaten des Schnittpunktes S von a) auf diese Grenzen. Danach untersuchen wir ihn darauf, ob er Eintrittspunkt ist. Wie wir nachher sehen werden, benötigen wir den Austrittspunkt nicht. Uns genügt die Strahlrichtung.
if (0 <= s.x && s.x <= r.x &&
0 <= s.y && s.y <= r.y)
{
Ist S Eintrittspunkt?
}Dies machen wir analog für alle Rechtecke.
Der
Um den Abstand in Blickrichtung zu erhalten, verwenden wir den
Richtungsvektor des Strahls und fragen uns: Um wieviel muss er
verlängert oder verkürzt werden, damit wir mit ihm vom Augpunkt
aus genau den Schnittpunkt treffen? In anderen Worten: Mit
welchem Faktor f müssen wir ![]() multiplizieren, damit gilt
multiplizieren, damit gilt
![]()
beziehungsweise
a.x + f*d.x = s.x
a.y + f*d.y = s.y
a.z + f*d.z = s.z
Dies ist ein überbestimmtes lineares Gleichungssystem, das
zum Beispiel im Falle dx die Lösung![]() 0
0
f = (s.x - a.x) / d.x
hat. Numerisch am stabilsten ist die Lösung mit dem größten
Wert im Nenner. Ist also zum Beispiel d.z > d.x
und d.z > d.y, so bestimmen wir f
durch
f = (s.z - a.z) / d.z .
Der Schnittpunkt mit dem kleinsten, f
ist nun der Eintrittspunkt S des Strahls.
Der Strahl soll nun von S aus die Voxel des Grauwertvolumens nacheinander durchlaufen, "um zu erkunden, was es in dieser Blickrichtung zu sehen gibt". Zuerst müssen wir eine Möglichkeit finden, zu bestimmen, welche Voxel in welcher Reihenfolge vom Strahl getroffen werden und welche Strecke der Strahl in ihnen zurüücklegt. Dies erledigen wir mit Hilfe einer Art dreidimensionalen Linienalgorithmus. Grauwert und Transparenz der betroffenen Voxel müssen in eine Rechnung einfließen, die uns schließlich die Farbe des Bildpixels liefert, durch den der Strahl geht.
Bevor ich mit diesen beiden Punkten fortfahre, möchte ich
einige Worte über die Transparenz der Voxel verlieren. Wir haben
die Möglichkeit, alle Voxel gleich transparent zu machen, doch
dies ergibt nur in wenigen Fällen wirklich Sinn: Dunkle Voxel,
die in der Computertomographie für Gewebe mit geringer Dichte
(im Extremfall Luft) stehen, verdecken dann hellere Voxel, also
feste Strukturen wie zum Beispiel Knochen. Daher bietet es sich
an, die Transparenz t eines Voxels von dessen
Grauwert I abhängig zu machen. Im Normalfall haben
dunkle Voxel eine höhere Transparenz als helle (Abb. 5).
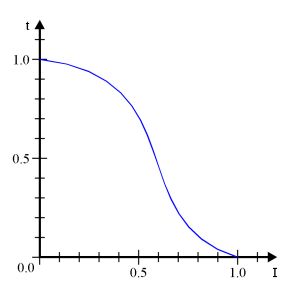
Abb. 5
Im einfachsten Fall setzt man sogar
t(I) = 1 - I
Was bedeutet nun eine Transparenz t von zum
Beispiel t = 0.5? Wir wollen es hier so auffassen,
dass ein Betrachter, wenn er entlang eines Strahls blickt, der
gerade (lotrecht) durch den Voxel hindurch geht, alles hinter dem
Voxel nur noch halb wahrnimmt (Abb. 6 rechts). Zur anderen
Hälfte nimmt der Pixel die Farbe des Voxels an:
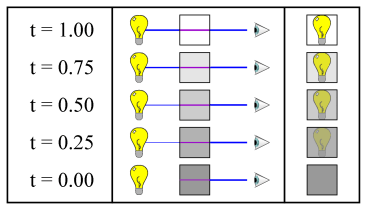
Abb. 6
Blickt der Betrachter schräg durch den Voxel, so ändert dies
zwar nichts an der Transparenz des Voxels, aber sehr wohl an dem,
was der Betrachter sieht. Setzen wir die Kantenlänge eines
Voxels auf 1 und sei len die Länge des Strahls
innerhalb des aktuellen Voxels (Abb. 7).
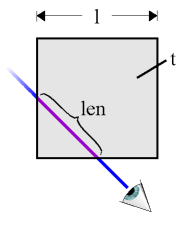
Abb. 7
Wir suchen nun einen Zusammenhang zwischen der Transparenz t
des Voxels, der Länge len des Strahls im Voxel und
der wirklichen Lichtdurchlässigkeit T, die der
Betrachter wahrnimmt. Wenn len = 0 ist, also der
Strahl nur die Kante des Voxels streift, sehen wir alles genau so
hell, wie es ist, d.h. T = 1. Für len
= 1, also den Fall, dass der Strahl den Voxel lotrecht trifft,
hatten wir T = t vereinbart (Abb. 8).
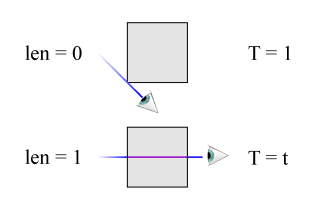
Abb. 8
Mit Hilfe dieser beiden Stützpunkte und einer einfachen linearen Interpolation erhalten wir:
T = (1 - len)*1 + len*t = 1 - len*(1 - t)
Nun müssen wir noch aufpassen, dass diese Durchlässigkeit T
nicht negativ wird (Abb. 9).
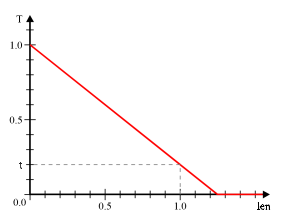
Abb. 9
Dies geschieht durch eine einfache if-Abfrage:
if (T < 0) T = 0;in C, also
if T < 0 then T := 0;in PASCAL.
Sehen wir uns an, wie ein Strahl durch unser anfänglich vorgestelltes Grauwertvolumen läuft. Die Voxel in Abbildung 10 sind in der Reihenfolge des Durchlaufens numeriert. Es fällt auf, dass jeder nachfolgende Voxel mit dem vorhergehenden Voxel eine Fläche gemeinsam hat. Wie wir sehen werden, läßt sich der Fall, dass der Strahl genau durch eine Ecke geht, als Spezialfall davon modellieren.
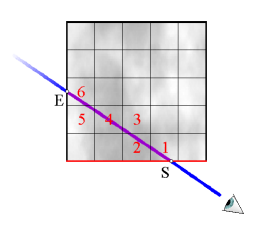
Abb. 10
Entscheidend sind also die Schnittpunkte des Strahls mit den Seitenflächen der Voxel. Wenn wir diese Schnittpunkte bestimmen können, wissen wir
Die Koordinaten V = [v.x, v.y, v.z]
des
Wie gehen wir vor? Wir runden zunächst die Koordinaten von S
ab. Für die x-Koordinate erhalten wir so den Wert 3, für die
z-Koordinate den Wert 5. Die y-Koordinate interessiert uns erst
einmal nicht, der Strahl verlaufe irgendwo parallel zur xz-Ebene.
Der abgerundete Wert v.z = 5 ist ein Spezialfall,
für den wir stattdessen v.z = 4 wählen müssen, um
eine gültige Voxelposition zu erhalten. Insgesamt ist also der
Startvoxel V = [3, -, 4].
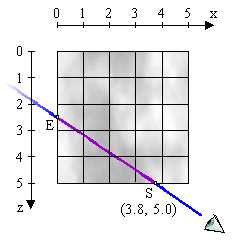
Abb. 11
Nennen wir die Länge des Quaders in Voxeln auf der x-Achse max.x
(in unserem Beispiel ist max.x = 5). Definieren wir
für die beiden anderen Achsen analog max.y und max.z,
so erhalten wir als Pseudocode für die Berechnung des
Anfangsvoxels im zweidimensionalen Fall:
v.x = floor(s.x);
v.y = floor(s.y);
v.z = floor(s.z);
if (v.x == max.x) v.x = max.x - 1;
if (v.y == max.y) v.y = max.y - 1;
if (v.z == max.z) v.z = max.z - 1;Dabei rundet floor(x) den Wert von x
auf die nächste ganze Zahl ab.
Wie geht es nun weiter? Wir sehen, dass jeweils an einem
Schnittpunkt des Strahls mit den Voxelgrenzen von einem Voxel in
den nächsten gewechselt wird. Vom Startpunkt aus wollen wir nun
bestimmen, welcher Voxel nach dem Voxel V = [3, -, 4]
durchschritten wird. Machen wir das erst einmal durch Hinsehen.
Ich werde später erklären, wie man es berechnet. Der erste
Schnittpunkt liegt auf einer d.x < 0), wird der
nächste Voxel [3, -, 3] sein. Jedes Mal, wenn wir
auf eine vertikale Voxelgrenze stossen, addieren wir also das
Vorzeichen der x-Komponente des Richtungsvektors ![]() (in unserem Fall
(in unserem Fall sign(d.x)
= -1) auf v.x. Wenn wir auf eine d.z
auf v.z. Für die y-Richtung, die nicht zu sehen
ist, gilt analoges.
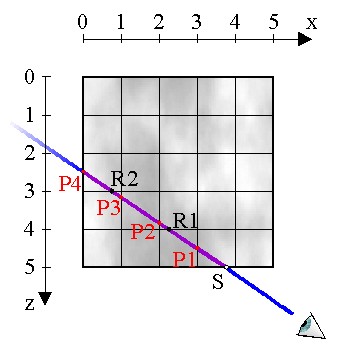
Abb. 12
Es gibt in unserem Beispiel Schnittpunkte P auf vertikalen (rot) und Schnittpunkte R auf horizontalen Voxelgrenzen (schwarz). Die dritte Art von Voxelgrenzen, die flach auf unserem Bild liegen, sehen wir nicht. Deshalb lassen wir sie vorerst außer Betracht. Wir bestimmen zunächst die Schnittpunkte P1 unr R1 mit der nächsten vertikalen und der nächsten horizontalen Trennebene auf dem Weg des Strahls. Danach wählen wir aus diesen beiden Schnittpunkten denjenigen aus, der unserer aktuellen Position (S) am nächsten liegt. Dies ist der Schnittpunkt, durch den der Strahl als nächstes geht, in unserem Beispiel P1. Danach setzen wir unsere aktuelle Position auf P1 und bestimmen P2. R1 bleibt ja weiterhin als Auswahlmöglichkeit gültig. Nun müssen wir also zwischen P2 und R1 den am nächsten zu P1 gelegenen Schnittpunkt aussuchen. Dies ist R1. Wir setzen unsere aktuelle Position auf R1 und bestimmen nun R2, usw. Auf diese Weise hangeln wir uns ganz durch das Grauwertvolumen hindurch.
Wenn V = [v.x, v.y, v.z] unsere aktuelle Position
im Grauwertvolumen ist, dann sieht der Teil des Algorithmus, der
die ersten Schnittpunkte findet, als Pseudocode so aus:
// Bestimme P neu:
if(d.x < 0) P = Schnittpunkt mit Ebene x = v.x);
else if(d.x > 0) P = Schnittpunkt mit Ebene (x = v.x + 1);
elseKein Schnittpunkt P vorhanden;
// Bestimme Q neu:
if(d.y < 0) Q = Schnittpunkt mit Ebene y = v.y);
else if(d.y > 0) Q = Schnittpunkt mit Ebene (y = v.y + 1);
elseKein Schnittpunkt Q vorhanden;
// Bestimme R neu:
if(d.z < 0) R = Schnittpunkt mit Ebene z = v.z);
else if(d.z > 0) R = Schnittpunkt mit Ebene (z = v.z + 1);
elseKein Schnittpunkt R vorhanden;
Die Frage, welcher Schnittpunkt als nächstes an der Reihe ist, lautet als Pseudocode:
if(P näher als Q) {
if(P näher als R)
// P ist nächster Schnittpunkt
v.x = v.x + sign(d.x);
Bestimme P neu;
else// R ist nächster Schnittpunkt v.z = v.z + sign(d.z); Bestimme R neu; }else{
if(Q näher als R)
// Q ist nächster Schnittpunkt
v.y = v.y + sign(d.y);
Bestimme Q neu;
else// R ist nächster Schnittpunkt v.z = v.z + sign(d.z); Bestimme R neu; }
Sobald eine der Koordinaten v.x, v.y
oder v.z aus dem gültigen Bereich hinausläft, sind
wir durch das Grauwertvolumen hindurchgelaufen und können
abbrechen.
Wenn wir uns noch einmal ins Gedächtnis rufen, was für
Informationen wir noch erhalten wollten, so erkennen wir, dass
uns die Schnittpunkte im einzelnen gar nicht interessieren,
sondern nur die Abstände zwischen ihnen. Es gibt eine einfache
Möglichkeit, nur den Abstand eines Schnittpunkts vom Startpunkt
S zu bestimmen. Dazu gehen wir wie folgt vor: Seien P
und R zwei Schnittpunkte. Wir wollen den Abstand
zwischen ihnen bestimmen. Dazu drücken wir P = (p.x,
p.y, p.z) und R = (r.x, r.y,
r.z) durch den Ortsvektor des Startpunktes S = (s.x,
s.y, s.z) und den Richtungsvektor des
Strahls ![]() = (
= (d.x,
d.y, d.z) aus. Mit zwei zu bestimmenden
Variablen f und g gilt dann
![]()
![]()
beziehungsweise
p.x = s.x + f*d.x;
p.y = s.y + f*d.y;
p.z = s.z + f*d.z;
r.x = s.x + g*d.x;
r.y = s.y + g*d.y;
r.z = s.z + g*d.z;
Es vereinfacht vieles, wenn wir ![]() normieren.
normieren. ![]() habe also die Länge 1. Nehmen wir nun an,
wir befänden uns am Schnittpunkt P und der nächste ermittelte
Schnittpunkt sei R. Wir suchen also die Länge
habe also die Länge 1. Nehmen wir nun an,
wir befänden uns am Schnittpunkt P und der nächste ermittelte
Schnittpunkt sei R. Wir suchen also die Länge len
von R-P. Wie wir sofort sehen, wird
len = g - f.
Alles, was wir nun noch brauchen, ist eine einfache
Möglchkeit, f bzw. g zu berechnen. Ich
möchte dies für die Punkte P, d.h. für die vertikalen
Trennebenen, zeigen (siehe noch einmal Abb. 12).

Abb. 12
Der Strahl tritt bei S im Voxel [3, -, 4] ein. Da er nach
links weist (d.x < 0), ist die vertikale
Trennebene (x = 3) die erste Ebene, mit der ich den Strahl
schneidem muss. Unser Ansatz für den ersten Schnittpunkt P1
lautet also
p1.x = s.x -f1*d.x = 3
Damit berechnen wir den ersten Faktor f1 zu
f1 = (s.x - 3) / d.xDer zweite Schnittpunkt P2 hat ganz analog den Faktor
f2 = (s.x - 2) / d.x
= (s.x - 3 + 1) / d.x
= f1 + 1/d.xGenauso wird für P3 der Faktor f3 zu
f3 = f1 + 2/d.xAllgemein:
fn = f1 + n/d.xDamit haben wir die Möglichkeit, einen sogenannten
inkrementellen Algorithmus zu formulieren. Inkrementell heisst
er, da bei jedem weiteren Schnittpunkt der Faktor um 1/d.x
erhöht wird. Für die Berechnung der Schnittpunktfaktoren in y-
und z-Richtung gehen wir analog vor.
Wir haben nun alle Informationen, die wir benötigen. Wie die Farbe des Pixels berechnet werden kann, ist kein großes Geheimnis mehr. Wir gehen die Voxel, die der Strahl trifft, einfach der Reihe nach durch und berechnen in jedem dieser Schritte ein wenig mehr dessen, was der Betrachter sieht. Betrachten wir den ersten Voxel mit einer Lichtdurchlässigkeit von z.B. T = 0.2, so sehen wir zu 80% die Farbe I des Voxels und zu 20% das, was dahinter liegt, d.h. die Voxel 2, 3, 4, usw. Wir berechnen also die Farbe F des Pixels aus
F = (1-T)*I + T*(Alles hinter dem Voxel)
Verallgemeinern wir das. Wenn I(k) die Grauintensität des k-ten durchlaufenen Voxels ist, und T(k) seine Lichtdurchlässigkeit, dann wird die Farbe F(k), die alles beinhaltet, was mit und hinter dem k-ten Voxel zu sehen ist, zu
F(k) = (1-T(k))*I(k) + T(k)*F(k+1)
F(1), ist die gesuchte Farbe unseres Pixels. Die Berechnung geht nicht endlos weiter, da der Strahl ja nach einem gewissen k wieder aus dem Volumen austritt. Es gibt sogar einen Grund, die Berechnungen noch vorher abzubrechen. Zum Beispiel, wenn wir auf einen undurchsichtigen Knochen treffen. Allgemein haben Voxel, die weiter hinten im Grauwertvolumen liegen, einen geringeren Einfluss auf die Farbe eines Pixels als weiter vorne liegende. Fragen wir uns hierzu: Welchen Einfluss kann der k-te Voxel hächstens noch auf die Farbe des Pixels haben?
An der obigen Rekursionsformel sehen wir, dass jeder weiter hinten liegende Farbwerte mit T(k) multipliziert werden. Die Intensität des zweiten Voxels wird also mit dem Faktor T(1) Einfluß auf die Farbe des Pixels nehmen, der dritte Voxel mit T(1)*T(2) usw. Allgemein wird der Einfluss E(k) des k-ten Voxels auf die Farbe des Pixels maximal T(1)*T(2)*...*T(n):
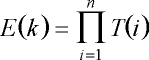
Sinkt dieser Einfluß unter einen gewissen Wert, führt die Berechnung folgender Pixel zu keiner Änderung der Pixelfarbe mehr. Das liegt daran, dass die Farbe eines Pixels z.B. aus 256 Graustufen besteht. Sinkt der Einfluß E(k) unter 1/256tel, so können wir die Berechnungen abbrechen. Ist keine solch hohe Qualität gefordert, reicht auch ein höherer Wert.
Wir können den Einfluss E(k) auch verwenden, um die Farbe des Pixels durch Addition kleiner Farbanteile zu gewinnen. Dabei Addieren wir zur Farbe F des Pixels in jedem Schritt k den entsprechenden Anteil der sichtbaren Voxelfarbe (1-T(k)) * I(k) hinzu, also
F = F + E(k) * (1-T(k)) * I(k)
Die einzelnen Schritte des Algorithmus hier noch einmal als Pseudocode formuliert.
Füralle Bildpixel (x,y)wiederhole{ // // Ermittle Eintrittspunkt S: //Füralle 6 Rechtecke Rwiederhole{ Schneide den Strahl (A,d) mit der Ebene von R -> Schnittpunt SWennder Schnittpunkt S innerhalb der Rechtecksgrenzen liegt
undEintrittspunkt ist,dannmerke S
}
F = 0 // Farbe des Pixels anfangs schwarz
WennEintrittspunkt gefunden
{
E = 1 // Einfluss des aktuellen Voxels
falt = 0 // Faktor des letzten Schnittpunkts (anfangs S)
//
// Durchlaufe das Grauwertvolumen ab S
//
Wiederhole bisder Einfluß E nicht mehr relevant ist
oderbis der Strahl das Grauwertvolumen verläßt
{
Ermittle die nächsten Schnittpunkte in x-, y- und z-Richtung
Ermittle daraus den nächsten Voxel in Richtung d
und den Faktor f des nächsten Schnittpunkts
len = f - falt
// I = Grauwert des Voxels
// t = Transparenz des Voxels
T = 1 - len*(1 - t)
Wenn(T <0) b>dann T = 0
F = F + E*(1-T)*I // Addiere Farbanteil zu Pixelfarbe
E = E * T // Halte Produkt auf dem Laufenden
falt = f
}
}
Zeichne Pixel (x,y) mit Farbe F
}
Für Echtzeitanimationen ist triplebuffering zu empfehlen, da der Rechenaufwand auf den heutigen Maschinen selten innerhalb eines Frames bleiben wird (war während der Erstellung des Artikels so). Natürlich könnte man aus demselben Grund anführen, dass Triplebuffering Speicherverschwendung ist, denn die Geschwindigkeitssteigerung ist nicht sehr groß. Dem halte ich entgegen, dass die Animation gleichmäßiger wird.
Herzlichen Dank an Andre Losanow für Hinweise auf Fehler im Text. Über Anregungen, Lob und Kritik freue ich mich sehr!
| [WATT89] | Alan H. Watt "Fundamentals of Three-Dimensional Computer-Graphics" Addison-Wesley Publishing Company, Reading, Massachusetts, 1989 ISBN 0-201-15442-0 (there is a second edition but I don't have it) |
Linien | Dreiecke | Volumendarstellung | Iteratives 3D Füllen